The Dall Null Test
Test Your Non-Spherical Optics Using a Simple Null Test
John D. UptonAugust 15, 1999
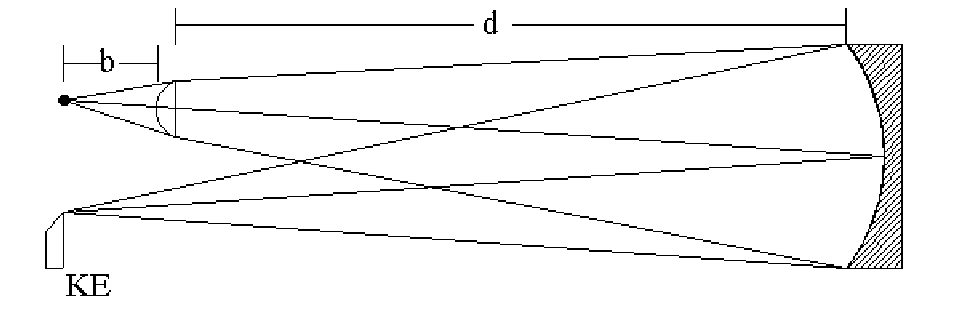
The relative ease of making spherical optical elements is made possible by the ease in testing them. Spherical optics may be tested at their center of curvature. When tested in this way, the optical element is finished when it nulls - its appearance is flat and devoid of telltale shadows under test. This same concept may be applied to many non-spherical surfaces using a variety of null tests. One of the easiest to implement and use is the Dall null test.
Introduction
A number of null tests for paraboloidal or other conic optical surfaces have been described. One is the Dall null test first described by Horace E. Dall a half century ago. Other well known null tests for conics include the auto-collimation test using a flat mirror, the Ross null test, and of course, the star test.
For spherical optical surfaces, the Foucault test conducted at the center of curvature is a null test. One looks for the condition of the whole surface darkening at once with no discernible shadows. This marks the null. The star test is a null test for paraboloids, but its use is better suited as a final check on a surface's figure than a routine test during early figuring.
Horace Dall (among others) noted that the introduction of a lens in the Foucault test between the pinhole light source and a paraboloidal surface under test could be used to add spherical aberration which is opposite in sign to that inherent in the surface tested at its radius of curvature. By carefully choosing the lens and setting the spacings between the pinhole, lens, and mirror, the two components of spherical aberration can be made to cancel one another. The Foucault test when modified in this way becomes a null test.
The Ross null test is another that is set up in a similar manner. A lens is introduced between the tester and the surface under test. The key difference between the Dall and Ross null tests is that in the Ross variation, the light transverses the lens twice. In the Dall null test, only the light from the pinhole passes through the lens. In the Ross null test, the lens must be of generally higher quality since light passes through it twice. In both tests, it may be required or at least desirable to use a beam splitter to avoid off axis astigmatic effects with fast surfaces. Astigmatism can be more of a problem in the Dall Null test since the returning beam must pass around the edge of the lens assembly. The effects of the off-axis nature of the test may be mitigated somewhat by arranging the tester such that the knife edge is either above or below the source / lens assembly. Each test has its good and bad points but are within the reach of amateurs.
History
Dall's article, first published in The Journal of the British Astronomical Association in November 1947, also appears in the book Amateur Telescope Making III (page 149) published in 1952. Today, the article may be found in Amateur Telescope Making 1 (page 315) in the edition republished by Willman-Bell in 1996. Daniel Malacara describes and analyses the Dall and other compensator tests in his classic treatise Optical Shop Testing on page 430. Further discussion of the Dall null test appeared in Sky & Telescope magazine in the September 1976 issue. That article also relates the extension of the Dall null test for non-spherical surfaces other than paraboloids.
It is unknown how many amateurs are familiar with the test or how many have used it. I believe the simplicity of the test warrants more widespread use within the amateur community. It presents a means for even the beginner to see and understand what is happening on an optical surface during figuring.
Implementation
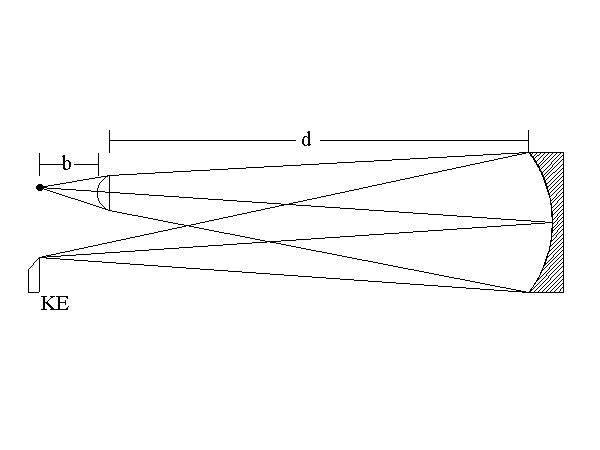
The diagram at right shows the set up of the Dall null test. It looks like the standard Foucault test set up with the addition of the small lens near the pinhole light source. A plano-convex lens is generally used since it is easier to set up a ray trace for that configuration. Once the focal length of the lens has been carefully measured, an index of refraction may be assigned assuming a common crown glass like BK7 whose n = 1.518722 at 546 nM. If you know the index of refraction of your lens, so much the better. As long as one side of the lens is flat, the radius of curvature of the other side may be calculated as R = (n - 1.0) x (focal_length + (center_thickness / n)).
This information is then entered into an optical design and ray tracing program or applied to a graph of Dall null test parameters as appears in the original write up. (The charts in the original article are only for use with paraboloidal mirrors.) Values of the pinhole to lens spacing b may then be determined. For the best null, a ray trace may be performed to determine the optimum lens to test surface distance d. If your tester is a "moving source" type, you should set up the test so that b + lens_thickness + d is equal the knife edge separation from the mirror. If you are setting up the Dall null test for a general conic surface, remember to input the proper conic constant into the ray trace program. Another article on this site describes how to set up the Dall Null test in the optical design program OSLO-EDU.
In practice, the spacings for a given test set up should always be ray traced to obtain the optimum values. In doing this, I have discovered that the best null may be obtained by setting up the lens with its convex side toward the mirror. This is opposite of the set up Dall recommends in the ATM article. This can make a significant difference in the quality of null obtained with faster mirrors. For example, a 16" F/4.5 mirror and 6" focal length lens when set up as recommended by Dall gives a null with a residual error of about 1/8 waveP-V or 1/32 wave RMS (0.962 Strehl). When the lens is turned around, a null of 1/11 wave P-V or 1/48 wave RMS (0.982 Strehl) may be obtained. Before deciding that this is the best approach, however, you should look at the tolerances involved with each method and how they differ. In general, the setup Dall recommended gives more latitude in tolerances. You should also note that Dall's setup will require a smaller lens.
Tolerances
The Dall Null Test has been said to be very critical in its set up and use. The tolerances in component spacings have at times been reported to be very tight. I suspect that this belief stems from the requirements of using a good lens more than anything else. One could reason that if the lens should be accurate to 1/8 wave or better, then the rest of the test parameters should be just as precise. My ray tracing of the test has shown that this need not be the case for many mirrors the ATM may produce. Only for large very fast mirrors do the tolerances become tight. Even then, with care, the amateur should be able to use the test to good advantage.
To look at the test's required accuracy, I set up two sample test configurations in the ray tracing program OSLO-EDU. The optics in question were both paraboloidal mirrors for Newtonian telescopes. In each case, I first used Dall's recommendation of having the flat side of the lens toward the mirror. I then repeated the tests with the lens turned around so that the convex side faced the mirror. The first configuration is a fairly typical 8" F/7 parabolic mirror. I chose a plano-convex lens of 6" focal length and 0.200" center thickness. This lens falls into the range of being 1/5 to 1/20 the focal length of the tested mirror as recommended by Dall. I assumed the lens to be made of BK7 crown glass. The second test used the same 6" lens against a 16" F/4.5 parabolic mirror.
I set up the ray-trace with light from the source passing through the lens the reflecting back from the mirror. I allowed the program to find the focal point of that setup. The lens to mirror distance was then adjusted so that the source and knife edge (focal point) were at approximately the same distance from the mirror. The program was then allowed to change to source to lens separation until it could minimize the total spherical aberration in the system. This marks the best null.
To read out the value of the null, the program was asked to refocus for minimum optical path difference and then display its value. To find the tolerances for the setups, one parameter was varied at a time until the Strehl ratio dropped to 0.800. The spacings were not optimized, only changed and then evaluated for degradation effects on the wavefront. The results are shown below.
In the first table below, we see the results with the 8" F/7 mirror. The second row of the table shows that with ideal spacings, the lens will null the parabolic mirror to approximately 1/145 wave P-V or 1/600 wave RMS (0.999+ Strehl), assuming a perfect lens and set up. This 6" focal length lens must be spaced about 3.277" from the pinhole for the desired null. The pinhole and lens assembly, in turn, will be spaced a little less than 107" from the mirror under test. Again, the tolerances indicated in this setup are for changing only one parameter at a time. Under these conditions, the lens needs to be at least 0.50" in diameter. Doubling this value allows just the center portion of the lens to be used, increasing the chances of meeting the typically recommended 1/8 wave surface criteria for the lens.
Mirror = 8" F/7
Lens convex side facing pinhole.
b =
f =
dia = 0.504"
d =
Ideal Values Strehl = 0.999
3.2769"
6.00"
106.70"
Tolerance: Strehl = 0.800
3.4658"
3.4658"
6.77"
5.63"
128.17"
96.51"
Tolerance As Percentage
+5.8%
-9.8%
+12.8%
-6.2%
+20.1%
-9.6%
When the lens is turned around so that the convex side faces the mirror, the following results are obtained. A better null is achieved given a perfect set up, but some leeway is lost in the tolerances allowed in the set up. The user must weigh these two factors in deciding whether to use this form of the test. It should also be noted that the lens must be larger when the convex side faces the mirror. In this case with the 8" F/7 mirror, the lens must be at least 0.9" diameter. Again, you should double this value unless you are very certain of the lens quality all the way to the edge.
Mirror = 8" F/7
Lens convex side facing mirror.
b =
f =
dia = 0.885"
d =
Ideal Values Strehl = 0.999
4.0224"
6.00"
103.60"
Tolerance: Strehl = 0.800
4.1774"
3.7462"
6.48"
5.77"
125.60"
93.09"
Tolerance As Percentage
+3.9%
-6.9%
+8.0%
-3.9%
+21.2%
-10.1%
As shown in the above tables, the lens to pinhole spacing may be varied considerably before the 0.800+ Strehl ratio null criteria is exceeded. It should be noted that you may err more on the short side than the long in the spacing of the lens. Next, the lens must have its focal length known to at least 7% when used in the recommended configuration. The lens to mirror spacing has plenty of leeway in both cases. This data shows that the 8" F/7 parabolic mirror is rather forgiving of set up using the Dall null test. This agrees with my own use of the test on a similar mirror.
In the second round of test simulations, a 16" F/4.5 mirror is used with the same 6" focal length lens. This same lens is still within the proper focal length range for this mirror as suggested by Dall though a little longer focal length would be desirable. Note that the lens requires a larger working diameter for the faster mirror. Again, it should really be about twice the specified size in practice. The first table shows the ray trace results for the lens set up as Dall suggests with the convex side facing the pinhole.
Mirror = 16" F/4.5
Lens convex side facing pinhole.
b =
f =
dia = 0.818"
d =
Ideal Values Strehl = 0.963
3.3395"
6.00"
138.50"
Tolerance: Strehl = 0.800
3.3674"
3.3084"
6.06"
5.94"
140.89"
136.39"
Tolerance As Percentage
+0.8%
-0.9%
+1.1%
0.9%
+1.7%
-1.5%
The table data shows that the tolerances are indeed much more strict for the larger, faster mirror. They are however, still within the skills of the ATM. Since these tolerances are somewhat cumulative, care should be taken to get everything set up as closely to specifications as possible. The closer you hold tolerances, the better the resulting null will be.
The next table below shows the effect of reversing the lens and obtaining a better null as mentioned before. As with the case of the 8" mirror above, the resulting null is now better, but the tolerances are somewhat tighter. The size of the lens has also grown considerably and may become a problem in setting up the test unless a beam-splitter is used. Care should be taken in choosing the set up you wish to use.
Mirror = 16" F/4.5
Lens convex side facing mirror.
b =
f =
dia = 1.446"
d =
Ideal Values Strehl = 0.982
4.0793"
6.00"
135.30"
Tolerance: Strehl = 0.800
4.1028"
4.0530"
6.04"
5.96"
137.85"
133.04"
Tolerance As Percentage
+0.6%
-0.6%
+0.7%
-0.6%
+1.9%
-1.7%
The strictest parameter in the Dall (or Ross) null test is the quality of the lens used. As mentioned, it is usually recommended that the lens be good to about 1/8 wave or better. In practice, most commercial lenses will probably meet this requirement over their central portion. By choosing a lens about twice as large as the required working diameter, you have a good chance of meeting this requirement.
One way to check your lens and tester construction is to set up the lens for the surface you will be working while the surface is still spherical. Remember that the Foucault Test is a null test for spherical mirrors. Set up the Dall null test with the spherical optical surface. The test will introduce the right amount of spherical aberration, but in the opposite direction. By examining the surface in this configuration and taking Foucault measurements, you should find that you have exactly the opposite amount of correction as will be required by the finished product. Your Foucault readings will indicate an oblate ellipsoid with the same correction as your desired paraboloid, but in the opposite direction. As long as the surface is close to being a good sphere, you should also be able to discern any zones or irregularities which may reside on the lens. If the lens passes this test, you are ready to proceed with using the Dall null test with confidence in your lens choice and tester setup.
Conclusions
As it is a null test, the Dall null test is not inherently quantitative. It cannot tell you how good your mirror is. It can only tell you when you are nearing completion. In addition, care must be taken in the test set up and the final results should be cross checked with an independent quantitative test. (Then you should also test the final system using the star test.)
The key advantage of the Dall null test is the ease with which you can gauge your progress toward the final figure. Under the test you see exactly where the hills, valleys, and other zones are on the optical surface. It allows you to get a quick, direct view of the condition of your work. The one time I used the test, I found that the interpretation of the shadows was very intuitive when you are working toward a null figure. I plan to use and recommend the test in the future, especially for smaller, moderate focal ratio optics.
So, next time you need to test a non-spherical surface, look through you junk lens box or surplus lens catalog, crank up your ray tracing software, and determine the parameters for the Dall null test. You may be surprised at how nicely it works.